Dessiner avec Fourier

MENU

INTRODUCTION

Considérons une courbe \(C\) du plan. Obtenir une représentation paramétrique de cette courbe c'est lui associer deux fonctions f et g définies sur une même partie \( D \subset \mathbb{R} \), telles que l'ensemble des points M(t) de coordonnées ( x(t) ; y(t) ) décrivent excatement \(C\) lorsque t décrit D. Par exemple le cercle de centre I et de rayon R admet comme représentation paramétrique $$\left\{ \begin{array}{rcl} x(t)=x_I+R \times cos(t)\\ y(t)=y_I+R \times sin(t) \end{array} \right.$$ Si je considère deux fonctions choisies disons au hasard, moyennant une étude de ces deux fonctions je peux obtenir l'allure de la courbe associée...
Cependant, j'ai longtemps pensé que le chemin inverse était impossible, c'est à dire dessiner une courbe au hasard sur une feuille, et obtenir une représentation paramétrique de cette courbe...,jusqu'au jour où je suis tombé sur une vidéo utube de El_Jj sur sa chaine 'Deux (deux ?) minutes pour en parler'.
Cette vidéo m'a littéralement scié car on y découvre qu'il est possible d'obtenir une approximation aussi fine que possible de n'importe quel lacet du plan...et tout ça grace aux Séries de Fourier...

LES SERIES DE FOURIER POUR LES NULS ( comme moi )

En général les Séries de Fourier font peur aux étudiants quand ils les découvrent en L2 ou en math spé.
Alors loin de moi l'idée de vous faire un cours complet sur les Séries de Fourier et ses applications, mais vous pourrez trouver ci-dessous mon cheminement personnel pour mieux appréhender ces fameuses séries...

En fait 'la théorie des séries de Fourier' ce n'est pas vraiment de l'analyse mais de la géométrie !

• L'espace des "fonctions de \(\mathbb{R}\) dans \(\mathbb{R}\) continues par morceaux et périodiques de période T", est un espace vectoriel. Nous noterons \(w = \frac{2 \pi}{T} \) leur pulsation.
• On peut munir cet espace vectoriel d'un produit scalaire : \( (f|g)= \frac{1}{T}\displaystyle \int_0^T f(t)g(t)dt\). Et ainsi en faire un EVN en posant \( ||f||^2 = (f|f)= \frac{1}{T}\displaystyle \int_0^T |f(t)|^2 dt\)
• Maintenant que l'on a un EVN, le top serait de trouver une Base orthonormée...alors on n'en a pas mais les fonctions \(c_n(t)=\cos(nwt)\) pour \(n \in \mathbb{N} \) et \(s_n(t)=\sin(nwt)\) pour \(n \in \mathbb{N}^* \) forment quant à elles une famille orthogonale infinie, ce qui est déjà vraiment bien !
  En effet, moyennant quelques calculs en trigonométrie, on obtient :
  • le produit scalaire de deux éléments distincts de cette famille est égal à \(0\)
  • \( (c_0 | c_0 )=1\)
  • Pour tout \(n > 0\), \( (c_n | c_n )=(s_n | s_n )= \dfrac{1}{2}\)

Quand \(f\) est un 'polynome trigonométrique'...

• Un polynome trigonométrique c'est juste une combinaison linéaire (finie) des éléments de notre famille orthogonale \(B\), quelque chose du genre : \( f(t)= \displaystyle \sum_{n=0}^N a_n.cos(nwt) + \displaystyle \sum_{n=1}^N b_n.sin(nwt)\)
• En calculant le produit scalaire de \(f\) avec tous les éléments de \(B\), on obtient :
  • \(a_0 = \dfrac{1}{T} \displaystyle \int_0^T f(t) dt\)
  • pour \(n>0 \) , \(a_n = \dfrac{2}{T} \displaystyle \int_0^T f(t) \cos(nwt) dt\) et \(b_n = \dfrac{2}{T} \displaystyle \int_0^T f(t) \sin(nwt) dt\)

Quand \(f\) N'EST PAS un 'polynome trigonométrique'...

1. On calcule quand même les coefficients :
   • \(a_0 = \dfrac{1}{T} \displaystyle \int_0^T f(t) dt\)
   • pour \(n>0 \) , \(a_n = \dfrac{2}{T} \displaystyle \int_0^T f(t) \cos(nwt) dt\) et \(b_n = \dfrac{2}{T} \displaystyle \int_0^T f(t) \sin(nwt) dt\)
2. On re-construit la combinaison linéaire, c'est la série de Fourier associée à \(f\) :
   \( S_Nf(t)= \displaystyle \sum_{n=0}^N a_n.cos(nwt) + \displaystyle \sum_{n=1}^N b_n.sin(nwt)\)
3. Pour chaque réel t, on fait tendre N vers \(+\infty\) et on utilise le théorème de Dirichlet pour obtenir la convergence vers \(f(t)\)

Conclusion

\(S_Nf(t) \) n'est que l'ombre de \(f\) projetée sur le 'mur' engendré par les premiers éléments de \(B\).
Quand le 'mur' grossit ( en dimensions), l'ombre est de plus en plus précise et coincide de plus en plus avec \(f\)

Dessiner un LACET avec les Séries de Fourier

Posons les bases

Un lacet du plan est une fonction \(\triangle\) continue de \([0,T]\) dans \( \mathbb{R}^2\), telle que \(\triangle(T)=\triangle(0)\). Nous noterons \(\triangle(t) = (X(t) , Y(t))\).

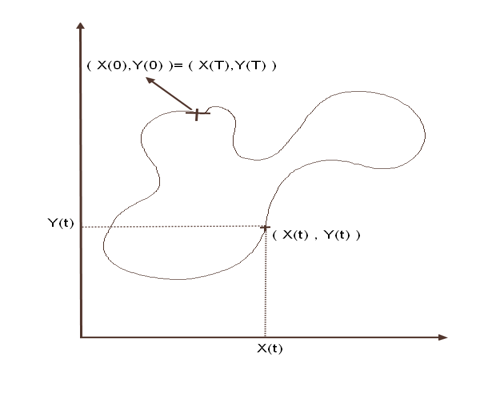
Si l'on prolonge \(\triangle\) sur \(\mathbb{R}\) en la dupliquant sur les intervalles de la forme \([kT,(k+1)T]\), \( \triangle\) devient une fonction continue et périodique sur \( \mathbb{R}\)
Les fonctions \(X(t)\) et \(Y(t)\) deviennent alors de bons candidats au théorème de Dirichlet...

Idée de l'algorithme

• On se fixe un rang N (qui sera le rang de la somme partielle)
• On effectue le tracé d'un lacet à la souris ( ou au stylet c'est encore mieux )
• Pendant le tracé, on récupère dans deux listes X et Y, les abscisses et les ordonnées de tous les points du tracé.
• On calcule jusqu'au rang N des approximations des coefficients de Fourier ( méthode des rectangles par exemple ) que l'on stocke dans les liste AX , AY , BX , BY
• Avec les coefficients stockés dans AX et BX, On fabrique la série \(S_X\) de Fourier approximant X
• Avec les coefficients stockés dans AY et BY, On fabrique la série \(S_Y\) de Fourier approximant Y
• Il n'y a plus qu'a relier les points \( (S_X(t) , S_Y(t) )\) pour obtenir le tracé de "l'ombre" du lacet initial

A vous de dessiner

Je vous laisse à disposition une feuille de dessin au format 16:9. (format d'écran le plus répandu aujourd'hui)
La longueur est de 800 pixel et la hauter est donc de 450 pixels.
Attention à bien dessiner un lacet !
Attention à ne pas dessiner trop vite, sinon le nombre de points sera insuffisant et des choses AFFREUSES et TERRIBLES se produisent !
Une fois terminé vous pouvez récupérer les équations paramétriques juste en dessous.

Une version OFFLINE

c'est ici pour la version Off Line