ACCUEIL MON ITCH.IO MA CHAINE ME CONTACTER

Le Rubix_Tore

En co-écriture avec Alexandre Bordas.
Je le remercie plus particulièrement pour la preuve du théorème final concernant le Rubix_Tore.

INTRODUCTION

Le Rubix_Tore d'ordre \(n\) peut se représenter à plat par un damier carré de \(n\) tuiles de coté, chaque tuile étant numérotée de \(1\) à \(n^2\).
Pour mélanger le Rubix_Tore, on peut effectuer quatre mouvements de base :

  • LEFT : déplace toute une ligne vers la gauche et téléporte la première tuile en fin de ligne à droite
  • RIGHT : déplace toute une ligne vers la droite et téléporte la dernière tuile en début de ligne à gauche
  • UP : déplace toute une colonne vers le haut et téléporte la tuile du haut en bas de la colonne
  • DOWN : déplace toute une colonne vers le bas et téléporte la tuile du bas en haut de la colonne



    • ON A DIT TORIQUE, PAS CARRE...

    Je vous annonce un "Rubix_Tore" et je vous donne des règles de déplacement de tuiles sur un carré...ça sens l'arnaque !
    Et pourtant pas dutout :

  • Les mouvements LEFT et RIGHT 'téléportent' les tuiles du carré ; c'est une facon de le convevoir, mais il en existe une autre : considérer que les deux bords gauche et droit du carré sont collés...ce qui donne un cylindre.
  • Les mouvements UP et DOWN, quant à eux permettent de recoller les deux bords du cylindre pour former un tore.

    • Dès lors, il n'y a plus de "téléportation" , mais les tuiles se déplacent sur un tore en 3 dimensions.



    VOICI LE RUBIX_TORE ( APLATI )

    Saurez vous vaincre le Rubix_Tore ?
    Je vous propose 5 niveaux de difficultés, du carré 2x2 au carré 6x6... amusez vous bien, et surtout ne cassez pas votre écran !



    REVISIONS SUR LE GROUPE SYMETRIQUE - \(RT_n\) le groupe des permutations du Rubix-Tore

    La littérature est plutot foisonnante au sujet du groupe symétrique, mais voici un lien vers quelques vidéos.

    Le Rubix_Tore est formé de \(n^2\) tuiles, et mélanger le Rubix_Tore c'est appliquer une permutation de \([|1,n^2|]\)

    L'ensemble de toutes ces permutations est le groupe symétrique \( (S_{n^2} , \circ )\). Il est constitué de \(n^2!\) éléments.

    Les mouvements 'LEFT'-'RIGHT'-'DOWN'-'UP' sont tous des permutations particulières de \(S_{n^2}\)
    Nous noterons :

    • \(R_1 , R_2 ... , R_n \) les mouvements 'RIGHT' sur chacune des n lignes
    • \(L_1 , L_2 ... , L_n \) les mouvements 'LEFT' sur chacune des n lignes
    • \(D_1 , D_2 ... , D_n \) les mouvements 'DOWN' sur chacune des n colonnes
    • \(U_1 , U_2 ... , U_n \) les mouvements 'UP' sur chacune des n colonnes
    Chacune de ces permutations est en fait un n_cycle, par exemple \(L_1 = \begin{pmatrix} 1&2&3&...&n\end{pmatrix} \)
    De plus les mouvements de type 'RIGHT' sont engendrés par les mouvements de type 'LEFT' et ceux de type 'DOWN' sont engendrés par ceux de type 'UP' puisque l'on a : \(R_i = L_i^{-1} = L_i^{n-1}\), et \(D_i = U_i^{-1} = U_i^{n-1}\)

    L'ensemble que nous noterons \(RT_n\) ( comme Rubix_Tore d'ordre n ) de toutes les configurations possibles du Rubix_Tore est donc le sous groupe engendré par les \(L_i\) et les \(U_i\).

    $$ RT_n= < L_i , U_i , i \in [|1,n|]>$$
    Cependant il faut faire attention au fait que les valeurs données dans les cycles ne sont pas les numéros sur les tuiles, mais leur position dans le carré.
    Traitons un exemple pour fixer les idées : plaçons nous dans \( RT_3\) et voyons ce que donne la composition \(U_1 \circ L_1 = \begin{pmatrix} 1&4&7 \end{pmatrix} \circ \begin{pmatrix} 1&2&3 \end{pmatrix} \).

    Nous avons \(U_1 \circ L_1 \begin{pmatrix} a&b&c\\d&e&f\\g&h&i\end{pmatrix} = U_1 \begin{pmatrix} b&c&a\\d&e&f\\g&h&i\end{pmatrix} = \begin{pmatrix} d&c&a\\g&e&f\\b&h&i\end{pmatrix}\)

    On obtient : \(U_1 \circ L_1 = \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\4&3&1&7&5&6&2&8&9\end{pmatrix} = \begin{pmatrix} 1&4&7&2&3\end{pmatrix} \)

    Maintenant que les bases sont posées, nous allons nous consacrer à un problème qui nous interesse vraiment : comment résoudre le Rubix_Tore ?



    RESOLUTION DU RUBIX_TORE

    Une idée naturelle est de se dire que pour résoudre le Rubix_Tore d'ordre n, il faut se ramener à résoudre le Rubix_Tore d'ordre n-1. Typiquement cette idée se traduit de la façon suivante :

    • Placer correctement les tuiles de la ligne 1 et de la colonne 1
    • Etre capable de modifier le reste du Rubix_Tore sans avoir à toucher à la ligne 1 et la colonne 1

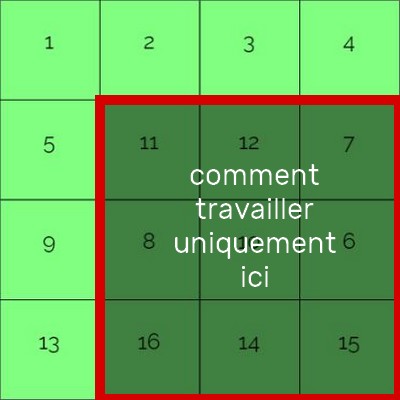
    Le problème est que nos cycles \(L_i\) et \(U_i\) sont "globaux" dans le sens où ils modifient une ligne ou une colonne entière nous interdisant de conserver intacte la ligne 1 et la colonne 1.
    Le défi est donc de fabriquer à l'aide de nos cycles de départ de nouvelles permutations "locales" laissant intactes la ligne 1 et la colonne 1.

    Alors comment créer une permutation 'locale en composant nos permutations 'globales' ?
    1. Il faut bien commencer par quelque chose, disons \(U_1\).
    2. Aucun intéret de le composer avec \(D_1\), car ça donnerait l'identité , et peu d'intéret de le composer avec un autre \(U_i\) car leur support sont disjoints, Du coup composons le avec \(L_1\) par exemple.
    3. Nous avons donc \(L_1 \circ U_1\), ce qui crée pas mal de désordre dans le Rubix_Tore, essayons de composer par leurs réciproques pour minimiser le désordre.
    4. Nous obtenons \(R_1 \circ D_1 \circ L_1 \circ U_1\) qui n'a aucune raison d'être l'identité puisque notre groupe de permutations n'est pas commutatif. Voyons ce que l'on obtient :
    $$R_1 \circ D_1 \circ L_1 \circ U_1 \begin{pmatrix} a_{11}&a_{12}&...&a_{1n}\\a_{21}& & &a_{2n}\\.& & &.&\\.& & &.&\\.& & &.&\\a_{n1}&a_{n2}&...&a_{nn}\end{pmatrix} = R_1 \circ D_1 \circ L_1 \begin{pmatrix} a_{21}&a_{12}&...&a_{1n}\\a_{31}&a_{22}& &a_{2n}\\.& & &.&\\.& & &.&\\a_{n1}& & &.&\\a_{11}&a_{n2}&...&a_{nn}\end{pmatrix}$$
    $$= R_1 \circ D_1 \begin{pmatrix} a_{12}&a_{13}&...&a_{1n}&a_{21}\\a_{31}&a_{22}& & &a_{2n}\\.& & & &.&\\.& & & &.&\\a_{n1}& & & &.&\\a_{11}&a_{n2}&...& &a_{nn}\end{pmatrix} = R_1 \begin{pmatrix} a_{11}&a_{13}&...&a_{1n}&a_{21}\\a_{12}&a_{22}& & &a_{2n}\\a_{31}& & & &.&\\.& & & &.&\\.& & & &.&\\a_{n1}&a_{n2}&...& &a_{nn}\end{pmatrix}$$
    $$=\begin{pmatrix} a_{21}&a_{11}&a_{13}&...&a_{1n}\\a_{12}&a_{22}& & &a_{2n}\\a_{31}& & & &.&\\.& & & &.&\\.& & & &.&\\a_{n1}&a_{n2}&...& &a_{nn}\end{pmatrix}$$
    Toutes les valeurs de la matrice de départ ont repris leur positions initiales sauf \(a_{11} , a_{12}\) et \(a_{21}\). Au final \(R_1 \circ D_1 \circ L_1 \circ U_1=\begin{pmatrix} 1&n+1&2\end{pmatrix}\)

    Et de façon général : \(R_i \circ D_j \circ L_i \circ U_j = \begin{pmatrix} (i-1)\times n+j&i \times n+j&(i-1) \times n+j+1\end{pmatrix}\)

    Nous avons l'exemple animé ci desous nous montrant que : \(R_2 \circ D_2 \circ L_2 \circ U_2 = \begin{pmatrix} 6&10&7\end{pmatrix}\)


    Tous ces 3_cycles ont la propriété d'être 'locaux' concentré sur 3 tuiles,laissant invariant toutes les autres tuiles.
    Les permutations que je vous propose ci-dessous sont toutes des 3_cycles, fabriquées sur le même modèle que \(R_i \circ D_j \circ L_i \circ U_j\)
    Ces 3_cycles sont indépendants de l'ordre du Rubix_Tore, et vont nous permettre de modifier des sous parties du Rubix_Tore sans toucher aux bordures déjà traitées.


    SEQUENCE 3_CYCLE LOCAL
    \( R_i \circ D_j \circ L_i \circ U_j \)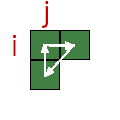
    \( (R_i \circ D_j \circ L_i \circ U_j)^{-1} = D_j \circ R_i \circ U_j \circ L_i \)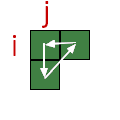
    \( R_i \circ U_j \circ L_i \circ D_j \)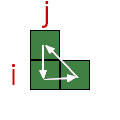
    \( (R_i \circ U_j \circ L_i \circ D_j)^{-1} = U_j \circ R_i \circ D_j \circ L_i \)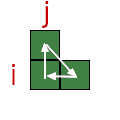
    \( L_i \circ D_j \circ R_i \circ U_j \)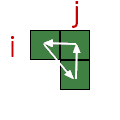
    \( (L_i \circ D_j \circ R_i \circ U_j)^{-1} = D_j \circ L_i \circ U_j \circ R_i \)
    \( L_i \circ U_j \circ R_i \circ D_j \)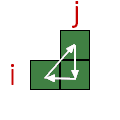
    \( (L_i \circ U_j \circ R_i \circ D_j)^{-1} = U_j \circ L_i \circ D_j \circ R_i \)

    En plus des \(2n\) mouvements de départ, nous avons réussi à rajouter 8 nouvelles familles de 3_cycles "locaux".
    Avec ces nouveaux outils vous devriez être en mesure de résoudre n'importe quel Rubix_Tore !
    La procédure est simple :
    1. Placer les tuiles de la ligne 1
    2. Placer les tuiles de la colonne 1
    3. Recommencer les étapes 1 et 2 avec le sous Rubix_Tore d'ordre n-1



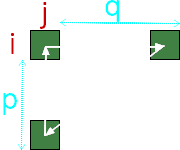
    POUR ALLER PLUS VITE

    Il existe d'autres cycles locaux qui vous permettront d'aller encore plus vite dans la résolution du Rubix_Tore.
    Ce sont des généralisations des 3_cycles que nous venons de décrire dans le paragraphe précédent.

    Par exemple \( R_i \circ D_j \circ L_i \circ U_j \) peut se généraliser de la façon suivante :

    \( R_i^q \circ D_j^p \circ L_i^q \circ U_j^p \) donne le 3_cycle
    Un autre exemple de 3_cycle local :
    \( R_i \circ D_j \circ L_i^2 \circ U_j \circ R_i\) donne le 3_cycle
    Que l'on peut généraliser de la façon suivante :
    \( R_i^p \circ D_j \circ L_i^{2p} \circ U_j \circ R_i^p\) donne le 3_cycle



    LE THEOREME DU RUBIX TORE

    Voici un théorème interessant concernant le Rubix_Tore :

    Soit n un entier supérieur ou égale à 2,
    • Si n est pair, alors le groupe des permutations du Rubix_Tore est le groupe symétrique tout entier : \(RT_n = S_{n^2} \)
    • Si n est impair, alors le groupe des permutations du Rubix_Tore est le groupe alterné : \(RT_n = A_{n^2} \)
    Vous pouvez lire la preuve ici.



    CONCLUSION

    Plus simple que son grand frère, le Rubix Cube, le Rubix_Tore a lui aussi ses qualités.
    Prochaine étape : trouver quelqu'un d'assez fou pour me contruire un Rubix_Tore en vrai...

    Retour MENU