Construction de polygones non croisés

MENU

INTRODUCTION

Ah les polygones, enfin un domaine simple des maths ! D'ailleurs on commence à entrevoir la notion de polygone dans les toutes petites classes, avant même de savoir lire on apprend à reconnaitre et à dessiner des triangles, des carrés et des rectangles !
Mais voici une question interessante me semble-t-il ?

Si l'on considère \(n\) points pris au hasard sur le plan, est-il possible de les relier de sorte à obtenir un polygone non croisé ?

Je suis un grand fan de ce genre de problème : très court à énoncer, très simple à comprendre, mais un peu plus délicat à traiter, et vous verrez que celui là, sans être insurmontable offre ses subtilités.
Mais avant même de s'attaquer au problème en lui même, d'autres questions me viennent à l'esprit :

NOMBRE DE POLYGONES A N SOMMETS

Considérons donc \(n\) points du plan \(A_1 , A_2 , ... , A_n\)
Combien de polygones différents peut-on construire à partir de ces \(n\) points ?

Partons du principe que construire notre polygone consiste à relier les points dans l'ordre dans lequel ils nous sont donnés, puis arrivé au dernier point on relie celui-ci avec le premier.
Dans ces conditions, le polygone \( (A_1 , A_2 , ... , A_n ) \) est le même que le polygone \( (A_2 , A_3 , ... , A_n, A_1) \) et plus généralement que le polygone \( (A_k , A_{k+1} , ... , A_n, A_1,...,A_{k-1}) \).

On peut donc fixer le point \(A_1\) comme premier point de notre polygone. Il reste donc \(n-1\) points à permuter ce qui fait \( (n-1)! \) permutations possibles.

De plus, si un polygone peut se construire en reliant les points dans un sens, alors il peut aussi se construire en reliant les points dans l'autre sens, c'est à dire que le polygone \( (A_1 , A_2 , ... , A_n ) \) est le même que le polygone \( (A_1 , A_n , A_{n-1} , ... , A_2) \)
Dans ces conditions le nombre de polygones ( croisés ou no ) que l'on peut obtenir avec n points du plan est \( \frac{(n-1)!}{2}\)

EXEMPLES POUR \(n=3\) et \(n=4\)

Cas \(n=3\)

Je vous laisse vous convaincre que pour \(n=3\) il n'ya qu'une seule et unique solution qui est le triangle !

Cas \(n=4\)

Considérons donc quatre points A,B,C et D, les trois polygones possibles sont : \( (A,B,C,D) \) - \( (A,B,D,C) \) - \( (A,D,B,C) \)
Ce qui donne lorsqu'on les dessine :
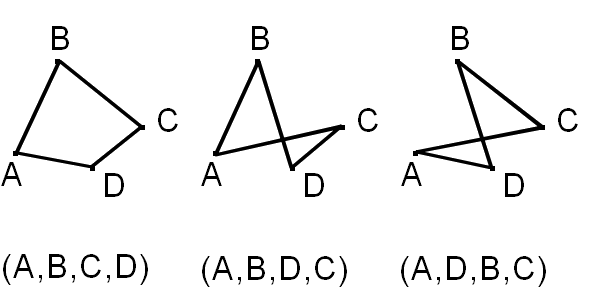On obtient alors un polygone non croisé et 2 polygones croisés.
Mais attention, la disposition des points est importante et peut changer beaucoup de choses. En effet si le point D est maintenant à l'intérieur du triangle ABC, les quadrilatères obtenus sont vraiment différents, mais surtout aucun d'eux n'est croisé !

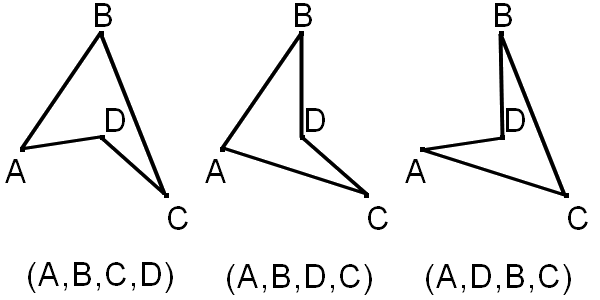
Le cas de n=4 , répond au questions que l'on s'est posé en introduction !

ALGORITHME DE CONSTRUCTION D'UN POLYGONE NON CROISE

On sait que l'existence de polygones non croisés n'est pas forcément unique, mais pour l'instant on ne sait pas s'il en existe forcément un...
D'ailleurs pour \(n=4\) on a bien trouvé un cas où il n'y a que des polygones non croisés, peut être est-il possible de trouver une disposition de points ( avec \(n \ge 5\) ) pour laquelle tous les polygones sont croisés, et dans ces conditions notre question de départ serait insoluble...
Pour résoudre notre problème, il suffirait de trouver un algorithme qui construit un polygone non croisé à partir de \(n\) points. On serait alors certain de l'existence d'au moins un polygone non croisé à n points.

Au final, je vous propose non pas un mais deux algorithmes de constructions d'un polygone non croisé.

Le premier commence par chercher la droite de régression linéaire de notre nuage de points de départ ce qui permet de couper le nuage en deux parties : les points du "haut" et les points du "bas". Il reste ensuite à ordonner les points de chacune de ces parties à l'aide d'une armée de produits scalaires et de gérer quelques cas particuliers à la marge...
Voici un lien utube pour voir le premier algorithme se construire pas à pas. Accrochez-vous , il y a 1h16 de vidéo !!!! :)

Le deuxième utilise le point moyen du nuage comme point pivot : on calcule les coordonnées polaires des points du nuage en prenant le point moyen comme centre du repère, puis on ordonne les points suivant l'angle qu'il font avec l'axe des abscisses. il ne reste plus ensuite qu-à relier ces points.
Voici un lien utube pour voir le deuxième algorithme se construire pas à pas.

CONCLUSION

Et voilà, nous somme arrivé à construire un polygone non croisé connaissant ses sommets !
Cependant, plusieurs questions restent en suspend, en voici deux :